In D/F V20N5 I asked for information about neural networks. Bruce Horrocks referred me to a work by Marvin Minsky and Papert Seymour (1) which deals with the mathematical theory. Andy Henstridge referred me to a more practical work, an OU text (2), which provides information for engineers on the architecture and operation of neural nets, precisely what I needed to write net programs for the HP49. Many thanks to both fellow members.
It has been very interesting to mug up the topic and I hope this account may be useful for other members. Certainly it seems that precious few have any better acquaintance with the subject than I had before this inquiry. One encounters occasional descriptions of neural networks but they are far too vague to give a useful idea of how they work.
Neural networks are arrays of simple units and act as classifiers. In general they are used to discover, by means of an output signal, whether or not an input signal to the network is a member of a certain subset of inputs.
Individual units are like the neurons of living nervous tissue in that they emit a simple signal (single digit or axonal impulse) in response to stimulation by similarly simple inputs. Their internal functioning is predetermined and there is no command or control module coordinating responses. In a learning net in a learning phase there is also a feedback arrangement to alter the operation of units and improve the performance of the net.
In this first part I shall describe three-layer, feedforward, hardlimited (ffhl) networks and all that follows herein relates to that topic. In a second part I shall deal with feedback learning. Many restrictions, complications and variations will remain unmentioned; anyone who wants more should consult ref (2). Our nets will be isolated from the real world but a useful net would need pre- and post-processor devices to form acceptable inputs and deliver meaningful results.

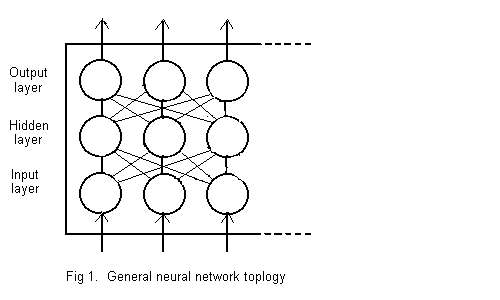
See Fig. 1.
Herein a neural network is an array of units in three groups -- an input layer, a hidden layer and an output layer.
The input signal for a net is a string of numbers (often binary), one for each unit of the input layer. Each unit repeats its input number unmodified to every unit of the hidden layer. There are at least as many input units as are necessary to represent all possible network inputs.
Each unit of the hidden layer receives a number from each input unit, computes a single binary digit output and delivers that to each cell of the output layer.
Each unit of the output layer receives a binary digit from each hidden unit, and computes a single binary digit and delivers that as its output. The output of the network is the string of outputs from its output units. There are at least as many output units as are required to represent possible net outputs (usually as binary numbers).
An input unit simply repeats its input signal unmodified to each hidden unit.
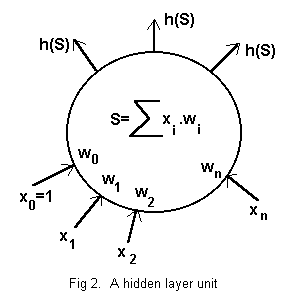
See Fig. 2. Each hidden unit has a real number weighting, w1 to wn, defined for each input, x1 to xn, from the n units of the input layer and an extra weighting w0 for a control input x0=1. The weighted sum
S = w0.x0 + w1.x1 + . . + wn.xn
of the inputs is computed and converted to a single binary digit by a ‘hardlimiting’ function as the unit’s identical signal to each output unit. The hardlimiting function ish(S) = 1 for S>=0, 0 for S<0
or sometimes
h(S) = 1 for S>0, 0 for S<=0
according to requirements. Only the first option is used herein.
Units of the output layer are exactly the same as those in the hidden layer except that the output is not repeated.
A simplest possible ffhl network has one unit in each layer and can function as a NOT gate, as shown in Fig. 3. The network input is 1 or 0. The weights of the hidden unit are w0=0.5 and w1= -1, giving a weighted sum S = x0.w0 + x1.w1 = 0.5 or -0.5. The hardlimiting function yields 1 for S>=0, 0 else. The output unit serves simply to transmit an unmodified signal so w0= -1/2, w1=1. Thus the binary input is inverted.
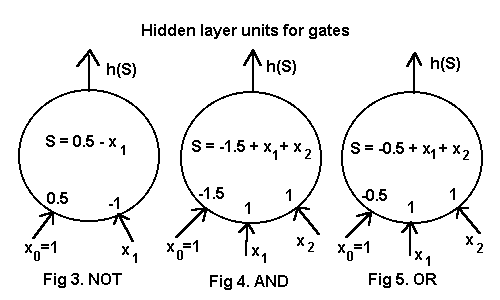
At the next stage of complication we shall have an extra input cell to accommodate the two digit input of an OR gate or an AND gate, as illustrated at Figs. 4,5. The AND gate reveals whether or not the input belongs to the set {(1 1)} and the OR gate similarly for the set {(1 0)(0 1)(1 1)}.
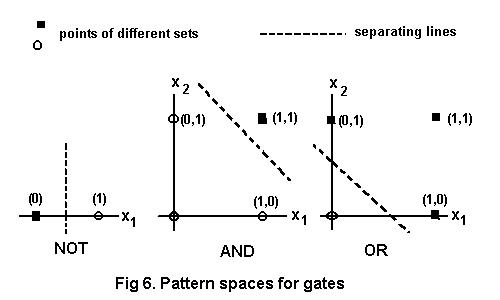
In the foregoing examples the possible inputs are linearly separable, as illustrated by the pattern spaces of Fig. 6. In such cases the separating line can be used to find weights for a network to discriminate between sets of points.
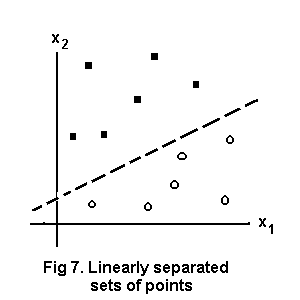
Consider the 2-D pattern space at Fig.7. We want a neural network to classify points (x1,x2) as belonging to the sets above or below the separating line. Take the same arrangement of units as for an OR gate and suppose the equation for any point on the separating line is
x2 = 0.5x1 + 2 (1)
The weighted sum for a point on the line would be
S = w0.x0 + w1.x1 + w2.x2 = w0 + w1.x1 + w2.x2 because x0=1 = 0 for a point on the separating line
whence
x2 = -(w1/w2).x1 - w0/w2 (2)
showing that -w1/w2 = 1/2 and -w0/w2 = 2 from (1) and (2).
Any consistent set of values will do so let w2=1, then the weights of the hidden unit are w1 = -1/2 and w0 = -2.
The output unit serves simply to transmit an unmodified signal so w0= -1/2, w1=1.
In general then, if w2 = 1 then w0 and w1 in a single hidden unit for a linearly separable problem are the additive inverses of the x2-axis intercept and the slope of the separating line respectively. Readers may check that this system works for the AND and OR gates.
In the last example weights have been found for a network which will generalise, giving a reliable output for any pair of real number input values.
More involved calculations would find weights for sets separable by functions of higher degree or in higher dimensional spaces but we shall not go that way. Sometimes a crafty dodge can be used to classify points which are not linearly separable, an XOR gate for instance, for which the pattern space is illustrated at Fig. 8.
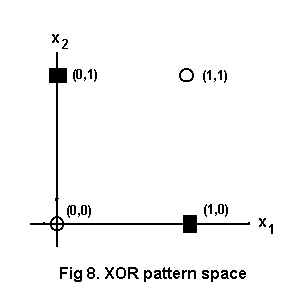
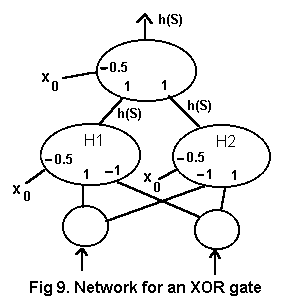
Two hidden units are needed, as shown in Fig. 9. Unit H1 outputs 1 for input (1,0). Unit H2 outputs 1 for input (0,1). The single output unit is an OR gate. A (1,1) input to the output unit is impossible so an OR gate output of 1 must mean XOR positive.
Readers are invited to find the weightings for an XNOR gate, returning 1 for two identical binary digits and 0 otherwise. It uses exactly the same network topology as the XOR; a set of possible weights is listed at (3).
The problem of finding weightings may be simplified by using more input units than necessary. Try to find weights for a network to deliver a 1 output if the second and fourth digits of a 5-binary-digit input string are both 1 and 0 output otherwise. Easy, honestly, no maths needed. Use five input units, one hidden unit and one output unit. A solution is offered at (4). It would be interesting to hear of any other applications devised by readers, particularly with more complicated network configurations.
The whole point of the exercise for me was to write neural net programs. A set of programs to operate ffhl nets follows.
Program ‘PREP’ prepares the units for any 3-layer feedforward hardlimited network. The function of each variable is shown by its INPUT string. Multiple input values are separated by spaces. Inputs and weighting values are stored as arrays; it was pleasant to realise that the weighted sums could be easily computed by matrix multiplication. A carriage return is needed in one of the INPUT strings. Approx mode must be checked.
%%HP: T(1)A(R)F(.);
« "PREP" DROP
"Enter no. inputs" "" INPUT OBJ-> 'Ino' STO
"Enter no. hidden units" "" INPUT OBJ-> 'Hno' STO 1 Hno
FOR j "Enter weights 0 to " Ino +
" for hidden unit " + j + "" INPUT OBJ->
NEXT
Hno 'Ino+1' 2 ->LIST ->ARRY TRN Hwts' STO
"Enter no. outputs" "" INPUT OBJ-> 'Ono' STO 1 Ono
FOR j "Enter weights 0 to " Hno +
" for output unit " + j + "" INPUT OBJ->
NEXT
Ono 'Hno+1' 2 ->LIST ->ARRY TRN 'Owts' STO »
Program ‘RUNIT’ gets and processes input using units set up by ‘PREP’, or otherwise. User INPUTs the network’s input signal at the prompt. Output is displayed as a list with the output of the first output unit at the head.
« "RUNIT" DROP 1 "Enter inputs 1 to " Ino + "" INPUT OBJ-> 1 'Ino + 1' 2 ->LIST ->ARRY Hwts * hardlimit [ 1 ] 1 COL+ Owts * hardlimit OBJ-> OBJ-> ->LIST DROP SWAP DROP ->LIST »
Program ‘hardlimit’ is called by ‘RUNIT’ to evaluate the binary output for a weighted sum using the hardlimiting function. As printed here it delivers 1 for a zero weighted sum.
« “hardlimit” DROP OBJ-> OBJ-> DROP SWAP DROP -> c « 1 c START 0 >= c ROLLD @ alter the test if desired NEXT 1 c 2 ->LIST ->ARRY » »
As an example to show these programs in action use them to set up the network to classify points in fig.7 above. Run ‘PREP’. Successive inputs will be
2 ENTER, 1 ENTER, -2 -0.5 1 ENTER, 1 ENTER, -0.5 1 ENTER
Now run ‘RUNIT’. 4 1 ENTER at the prompt yields 0 for a point below the line, 1 4 ENTER yields 1 for a point above the line.
So now we have some awkward ways to do things that can be done far more easily in other ways on an HP48/49 but the material in this part is essential preparation for the learning networks in Part II.
The source code for the programs in this article can be downloaded from Peter Gatenby’s web site at http://www.freenetpages.co.uk/hp/pvg or HPCC’s web site here
____________________________
(1) Perceptrons, an introduction to computational geometry. Expanded edition, by Marvin Minsky and Papert Seymour. MIT Press, 3rd printing 1988. ISBN 0-2672-63111-3(pbk).
(2) Concepts in Artificial Intelligence; Building Intelligent Machines, Vol. 2 by Jeffrey Johnson & Philip Picton. Butterworth-Heinemann/Open University, 1995. ISBN 0-7506-2403-5.
(3) Weightings for XNOR are:-
Hidden -1 0.5 0.5 and 0.5 -1 -1 Output -0.5 1 1
(4) Weightings for the 5 digit problem are:-
Hidden -2 0 1 0 1 0 Output -0.5 1
| pvg@mail.freenet.co.uk | Page last modified : 19th April 2002 |